La logica matematica del 1800 si collega direttamente ai lavori di Leibniz, egli come è noto ha tentato di dar corpo al sogno medievale di Raimondo Lullo a differenza del primo però il filosofo di Lipsia tentò di costruire una sintesi algebrico formale attraverso l'istituzione di un linguaggio formalizzato da lui detto caratteristica universale https://content.wolfram.com/uploads/sites/43/2013/05/4-large-a.png e attraverso un sistema di regole coerenti che si ritrovano in parte nel testo del 1666 Dissertatio de arte combinatoria. Nel tentativo di elaborare questo ambizioso progetto Leibniz si cimentò anche nel codificare l'algebra in un sistema binariohttp://www.istitutoalberghieroteano.edu.it/matealberghiero/images/numerazionebinaria.png e comprese che si poteva rappresentare la logica sillogistica di Aristotele attraverso gli insiemi https://image.slidesharecdn.com/sillogismoppt-130806053809-phpapp02/85/il-sillogismo-1-320.jpg?cb=1665587074. Nel corso del XVIII secolo molti studiosi proposero tentativi analoghi a quello intrapreso da Leibniz ma non riuscirono ad andare oltre ai risultati del filosofo tedesco. Tra questi personaggi possiamo citare solo a titolo informativo Johann Heinrich Lambert e Godefroy Ploucquet e per quanto concerne l'utilizzo degli insiemi in logico Leonhard Eulero (il cui lavoro sarà ripreso e completato dal logico inglese John Venn).
Il primo innovatore rispetto alla logica leibniziana fu Augustus De Morgan (1806- 1871), che può essere considerato il fondatore della logica della relazioni, ovvero l'algebralizzazione della logica, che sta alla base della futura logica-matematica. Scozzese di origine nacque a Madras in India nel giugno del 1806, studiò al Trinity College a Cambridge e nel 1828 divenne professore al London University Collegehttps://www.ilwindia.com/wp-content/uploads/2019/07/University-College-London-UK-1.jpg, tra le altre cose fondò la società di matematica di Londra nel 1866. Il suo contributo può essere riassunto nell'aver per primo applicato alla logica le tecniche algebriche, egli sostenne che la logica è il frutto di operazioni su simboli in base a regole di combinazione così come lo per la matematica, questo indirizzo lo portò a formulare due leggi importantissime dette appunto leggi di Morgan. Le leggi di Morgan possono essere riassunte in questo modo:
1) la prima legge afferma che negare la congiunzione di due proposizioni “non (piove e è giorno)” equivale a fare la disgiunzione delle due proposizioni negate “o(vel) non piove o(vel) non è giorno”.
2) la seconda legge afferma che negare la disgiunzione di due proposizioni “non (piove o è giorno)” equivale a fare la congiunzione delle due proposizioni negate “non piove e non è giorno”.
Queste leggi per onor del vero erano stata già trattate dalla logica proposizionale degli stoici, ma il modo in cui sono presentate da De Morgan rimane originale, inoltre la logica stoica sarà analizzata in modo rigoroso solo nel 1953 e dunque è probabile che De Morgan non conoscesse i risultati degli stoici.
Dal punto di vista formale possiamo scrivere le sue due leggi come segue:
| ¬(a∨b)⇔¬a∧¬b |
| non a o b se e solo se non a e non b |
| ¬(a∧b)⇔¬a∨¬b |
| non a e b se e solo se non a o non b |
Se vogliamo possiamo anche visualizzare le due leggi usando l'insiemistica:
Se pur circoscritto nei risultati il lavoro di De Morgan aprì la strada all'algebra di George Boole.
George Boole (1815-1864) nacque in Inghilterra a Lincoln in una famiglia di origini umili. Il padre era un ciabattino il quale tuttavia aveva trovato un'associazione culturale nella sua città dove poter coltivare la sua passione per la scienza è la tecnologia. Grazie all'accesso ai libri della biblioteca dell'associazione paterna Boole da autodidatta riuscì ad apprendere la matematica avanzata e dopo aver svolto per qualche anno l'attività di insegnante in scuole private venne chiamato ad insegnare alla Queens College di Cork in Irlanda. https://www.educationtrainingnetwork.com/magazine/wp-content/uploads/2019/02/DSC04353-min-933x445.jpg Dopo essersi costruito una solida reputazione di matematico, ancorché di logico, entrò in contatto con Augustus De Morgan, i suoi lavori più importanti sono L'analisi matematica della logica del 1847 e Un indagine sulle leggi del pensiero del 1854.
L'algebralizzazione della logica compiuta da Boole si fonda su una semplice trasmutazione dei valori semantici che possono assumere le proposizioni, in altre parole i valori di verità: vero o falso. Boole sulle stesse orme di Leibniz attribuì il valore algebrico di 1 alla verità e il valore algebrico di 0 alla falsità.
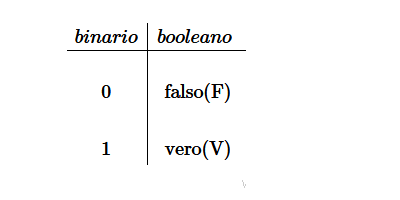
Dopo aver computato (calcolato) i valori semantici passò alla computazione della sintassi logica ovvero le leggi necessarie a tradurre le operazioni logiche che si effettuano con i connettivi in operazioni di tipo algebrico. Le principali sono:
L'addizione logica
La somma logica di due valori booleani è 1 (cioè la proposizione composta è vera) se almeno uno dei due fattori è uguale a 1 (cioè se almeno una delle due proposizioni semplici è vera).
Moltiplicazione logica
Il prodotto logico di due valori booleani è 1 (cioè la proposizione composta è vera) soltanto se entrambi gli addendi sono uguali a 1 (cioè se tutte e due le proposizioni semplici sono vere).
Complemento logico
Il complemento logico è l'operazione di negazione del valore booleano. E' indicato con un trattino sopra la variabile ed equivale a sottrarre al valore 1 (verità) se stesso.
Facciamo alcuni esempi prendiamo in esame il complemento logico ovvero la negazione, essa è un'operazione che nega una verità producendo falsità o nega una falsità restituendoci la verità, operando con alcune leggi dell'algebra binaria di Leibniz si può tradurre espressioni come "non è vero che piove" con 1-1=0 dove 1 sta per l'espressione "piove"...in linguaggio comune si potrebbe dire che "sottrarre al fatto di piovere il piovere" equivale ad affermare che l'affermazione "piove" è falsa.
Per quanto riguarda la moltiplicazione logica ovvero la congiunzione possiamo tradurre una proposizione complessa del tipo “piove e è giorno”, ammesso che entrambe le proposizioni semplici siano vere, con 1•1=1 e vedremo con altrettanta semplicità che se una delle due affermazioni è falsa (valore 0) otteniamo una proposizione complessa falsa infatti 1•0=0 perché se "piove e non è giorno" è chiaramente falsa la proposizione "piove e è giorno".
| operatore di prodotto logico AND | 1•1=1 |
| 1•0=0 | |
| 0•1=0 | |
| 0•0=0 | |
| operatore di somma logica OR | 0+0=0 |
| 1+0=1 | |
| 0+1=1 | |
| 1+1=1* | |
| operatore di complementazione logica NOT | ¬1=0 |
| ¬0=1 |
*Questi assiomi vanno accettati nella logica booleana e quindi non si devono interpretare secondo le regole matematiche abituali (sarebbe in questo caso assurdo porre 1 + 1 = 1)
http://www.dacrema.com/Informatica/Algebra_Boole.htm
In buona sostanza l'algebra booleana è uno strumento che traduce le operazioni logiche in operazioni algebriche, e avvalendosi dell'algebra binaria, delle operazioni algebriche in operazioni logiche.
Grazie alla sua algebra George Boole comprese che si poteva descrivere con le stesse equazioni sia la logica sillogistica sia quella proposizionale https://images.treccani.it/enc/media/share/images/orig/system/galleries/Enciclopedia_della_Matematica/fig_appendice_storia_matematica_034.jpg . Questi studi portarono l'attenzione dei matematici verso un'altra branca della logica matematica ovvero l'insiemistica che permetteva di descrivere entrambe le logiche.
https://miro.medium.com/max/724/1*sMxiKxm3scrh2_MKggvPJg.jpeg
L'altro grande contributo alla nascita della logica matematica, che nuovamente prende avvio dagli studi compiuti da Leibniz, è quello del matematico e logico tedesco Georg Cantor il quale ha concepito la teoria degli insiemi come base comune dell'aritmetica e della logica.
Georg Cantor, una delle maggiori intelligenze del diciannovesimo secolo (Russell, Autobiografia), nacque il 19 febbraio 1845 a San Pietroburgo. Nel 1856 si sposta con la famiglia a Francoforte a causa della salute precaria del padre; qui, malgrado i tentativi del padre di fargli studiare ingegneria, coltiva la sua attitudine verso le discipline matematiche. Nel 1863, dopo la morte del padre, inizia a frequentare l'università di Berlino, ove si applica alla fisica, alla matematica e alla filosofia. Ebbe diversi maestri, fra i matematici Weierstrass, Kummer e Kronecker. Sotto l'influenza di quest'ultimo si laureò nel 1867 e ottenne la libera docenza. Sotto l'influenza di Weierstrass i suoi interessi si spostarono verso la teoria delle funzioni, concentrandosi in particolare sul problema della rappresentabilità di una funzione in serie trigonometrica. Nel 1871 viene chiamato come docente straordinario ad Halle dove inizia a lavorare alla teoria degli insiemi. Nel 1879 diviene ordinario, sempre ad Halle, e nel 1884 compare la prima manifestazione della malattia nervosa che a più riprese si ripresenterà e che lo condurrà alla morte, avvenuta nella clinica psichiatrica di Halle nel 1918.
La fama di Cantor è legata a tre ambiti di ricerca che sono a loro volta collegati fra loro:
1) il primo riguarda la definizione di numero reale, i numeri reali erano il fulcro del calcolo infinitesimale, che grazi al lavoro di Carl Weierstrass intorno alla metà dell'800 non era più una semplice tecnica come, concepita da Leibniz e Newton, ma viveniva una vera e propria scienza matematica. Georg Cantor che era suo allievo e contemporanemente Richard Dedekind (allievo di Gauss) mostrarono nel 1872 che il concetto di numero reale e tutti i teoremi su di esso fondati derivavano dal concetto di numero naturale e dalle rispettive proprietà di questi, che risultavano essere dunque il fondamento di tutta la matematica. http://www.arrigoamadori.com/lezioni/StruttureMatematiche/Numeri/LaRett01.gif
https://www.sosmatematica.it/wp-content/uploads/2019/10/NumeriReali-300x300.png
https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcQn1jmcGhJaMbX--G6F48BK58WOIXGsIUb3WQ&usqp=CAU
2) il secondo riguarda il fondamento di una nuovo ramo della matematica che risulterà decisivo sia per l'analismi matematica quanto per la logica e la filosofia del linguaggio La teoria degli insiemi. La teoria aveva i suoi precursori in Galileo e Leibniz, e in particolare con il matematico Bernard Bolzano (1781-1848) divenne un ambito di studi e finalmente una teoria logico-matematica compiuto con Cantor. https://www.okpedia.it/data/okpedia/unione-degli-insiemi.gif
3) il terzo gli studi sulle proprietà dell'infinito attuale https://www.repstatic.it/content/nazionale/img/2020/02/16/232533061-cd25456f-cddf-4f94-b34b-73369d360c85.jpg
Tralasceremo il primo punto che risulterebbe ostico a chi non è un matematico e rimandiamo all'enciclopedia Treccani on line per chi volesse vedere la definizione di numero reale e la sua formula, tuttavia vale la pena dire che esso è fondamentale per gli autori del logicismo (Cantor, Frege e Russell) https://filosofiacatracha.files.wordpress.com/2016/01/gottlob_frege-russell.jpg?w=640 che tentarono di fondare la matematica sulla logica, si evince di conseguenza che esso è indissolubilmente collegato con la teoria degli insiemi che è appunto la teoria che permette di definire i concetti base della matematica in termini puramente logici.
Per quello che riguarda la teoria insiemistica di Cantor possiamo affermare che essa poggia interamente su due soli principi: il principio di comprensione e il principio di estensionalità.
In base al principio di comprensione ogni proprietà determina un insieme costituito da tutti e soli gli oggetti che godono di quella proprietà. https://pianetabambini.it/wp-content/uploads/2018/12/Esercizi-Insiemi-3.png Per esempio alla proprietà essere un albero corrisponde l’insieme degli alberi, e alla proprietà di essere una figura delimitata da tre lati corrisponderà l'insieme dei triangoli.
Ogni proprietà ha un estensione ovvero un numero di oggetti che gode di quella proprietà, se nessun oggetto gode di quella proprietà avremo comunque un insieme detto insieme vuoto. https://lafinestrasullalbero.it/wp-content/uploads/2016/11/0.png
Il principio di estensionalità afferma che due insiemi che hanno gli stessi elementi sono uguali questo vale per esempio per l'insieme dei triangoli equilateri e per l'insieme dei triangoli equiangoli. https://lafinestrasullalbero.altervista.org/wp-content/uploads/2016/11/uguale.png?w=300
A partire da queste due proprietà Cantor è riuscito a dare una definizione puramente insiemistica del concetto di numero naturale senza fare ricorso all'idea di numero o di quantità. Per definire il concetto di numero Cantor sia valso della relazione detta di equipotenza: due insiemi A e B sono chiamati equipotenti quando sono in corrispondenza biunivoca. http://www.andreaminini.org/data/andreamininiorg/insiemi-equipotenti-esempio.gif Ciò significa che è possibile associare ogni elemento di A uno e uno soltanto degli elementi di B e viceversa. Da ciò segue che il numero cardinale di un insieme A è l'insieme di tutti gli insiemi che sono equipotenti ad A.
Con l’opera di Cantor si è concluso il percorso iniziato da Leibniz che porta alla nascita della logica matematica, e che cerca di creare un legame stretto tra le regole del pensiero e quelle della matematica, riaccendendo il dibattito sul pitagorismo e il platonismo, va ricordato infatti che Cantor crede fermamente nell’esistenza autonoma degli enti matematici. https://thumbs.dreamstime.com/z/gruppo-di-base-dei-personaggi-cartoni-animati-numeri-121061867.jpg
Nella formulazione della teoria degli insiemi Cantor si pose il problema di distinguere tra insiemi finiti ed insiemi infiniti. https://silvanodonofrio.files.wordpress.com/2016/06/insieme.jpg?w=300 Da sempre l’infinito aveva generato difficolta insormontabili come quelle legate ai paradossi di Zenone https://www.cronachedalsilenzio.it/wp-content/uploads/2018/02/Achille-e-la-tartaruga.jpg e tale concetto era stato ostracizzato dagli antichi e dai medioevali. Tali problemi erano stati solo parzialmente risolti dal calcolo infinitesimale di Newton e Leibniz. Uno dei problemi irrisolti era ben rappresentato dal paradosso trovato da Galileo nel ‘600. Egli aveva mostrato che presa una circonferenza ed una più piccola concentrica alla prima, malgrado la seconda abbia una grandezza minore, ogni punto della circonferenza più grande trovava posto in quello più piccola. https://www.youmath.it/images/stories/AAArisposte/sub-dr/cerchi-concentrici/cerchi-concentrici.png In termini di teoria degli insiemi esse potevano essere messe in corrispondenza biunivoca.
Cantor insieme a Richard Dedekind (1831-1916) giunse a definire:
-un insieme è infinito quando è equipotente ad un suo sottoinsieme ovvero quando gode della proprietà di poter essere messo in corrispondenza biunivoca con una sua parte propria.
-un insieme è finito quando NON è equipotente ad un suo sottoinsieme ovvero non gode della proprietà di poter essere messo in corrispondenza biunivoca con una sua parte propria
Questa è una definizione fortemente contro-intuitiva perché mostra una equipotenza tra due insieme di cui uno appare chiaramente più grande del secondo. In sostanza veniva messa in discussione una delle fondamentali nozioni comuni degli elementi di Euclide che afferma che il tutto è maggiore della parte. La grande intuizione di Cantor è che sia necessario definire rispetto a cosa si può dire che una cosa sia uguale ad un'altra. Ovvero bisogna distinguere se si tratta di una uguaglianza in base alla numerabilità oppure in base alla dimensione. Mentre per dimensione i due insiemi sono diversi, sono uguali per numerabilità, in conclusione sono equipotenti ma non identici.
Sulla base di quanto affermato da Cantor i numeri naturali sono i numeri cardinali di insiemi finiti. Va notato però che l'insieme dei numeri naturali è infinito. https://www.lezionidimatematica.net/Insiemi_N_Q_R_Z/immagini_lezioni/lezione_03/im_01.png Essendo il numero naturale il numero cardinale di un insieme, qual'è sarà il numero cardinale dell'insieme infinito?
Cantor ha proposto di chiamare il numero cardinale di tutti gli insiemi che sono equipotenti all'insieme dei numeri naturali ℵo (Aleph con zero). https://i1.sndcdn.com/avatars-000480224064-07ltnu-t500x500.jpg Ma come si è visto sembra che esistano diversi tipi di infinito ed è legittimo chiedersi se tutti hanno lo stesso numero cardinale. Per secoli si è creduto che il concetto di infinito fosse un concetto limite ed invece Cantor dimostrò che vi è una cardinalità anche degli infiniti.
Ciò che io sostengo [...] è che oltre al finito c'è un transfinitum (ma lo si potrebbe chiamare anche suprafinitum), cioè una scala illimitata di modi determinati che per loro natura non sono finiti ma infiniti e però possono essere specificati, proprio come il finito. mediante numeri determinati, ben definiti e distinguibili l'uno dall'altro (Cantor, La formazione della teoria degli insiemi. Scritti 1872-1899)
Cantor mostrò che esistono almeno due diversi tipologia di "infinitudine": quello dei numeri naturali che definito come "numerabile" e quello dei numeri reali definito come "continuo". Mentre il secondo può descrivere i punti di una retta (ipotesi del continuo) il primo no.
Questo fu dimostrato tramite quello che viene definito argomento diagonale. Ragionando per assurdo supponiamo che l'insieme dei numeri naturali (0,1,2,3,...) e l'intervallo 0-1 che contiene tutti i numeri reali maggiori di 0 e minori di 1 siano equipotenti (proprietà che indica quando due insiemi sono uguali); si procede assegnando un numero naturale ad ogni intervallo presente tra 0-1. Ogni numero dell'intervallo è rappresentato da un numero decimale con infinite cifre es: 0,n1n2n3...
Dopo aver assegnato un numero naturale ad ogni numero dell'intervallo avremo la seguente corrispondenza biunivoca:
| 0 | = | 0, | n00 | n01 | n02 | .... |
| 1 | = | 0, | n10 | n11 | n12 | .... |
| 2 | = | 0, | n20 | n21 | n22 | .... |
| 3 | = | 0, | n30 | n31 | n32 | .... |
| .... | = | .... | .... | .... | .... | .... |
Da questa disposizione possiamo tuttavia individuare un nuovo numero reale sempre compreso nell'intervallo 0-1 che chiameremo numero diagonale
| 0 | = | 0, | n00 | n01 | n02 | .... |
| 1 | = | 0, | n10 | n11 | n12 | .... |
| 2 | = | 0, | n20 | n21 | n22 | .... |
| 3 | = | 0, | n30 | n31 | n32 | .... |
| .... | = | .... | .... | .... | .... | .... |
Come visibile questo numero, pur appartenendo all'intervallo 0-1, non è associato ad alcun numero naturale, ne segue che non è possibile stabilire una corrispondenza biunivoca tra l'insieme dei numeri naturali e l'intervallo di numeri reali presi in esame non è possibile. https://img.googl-info.com/storage/big/43973.jpg?8c1495409c0e3bf18d45a5e5da7b02a8=7ffb8e7a477588f474fdabf78c9c5fcd A seguito di questa dimostrazione Cantor inviò all'amico Richard Dedekind il 29 giugno del 1877 una lettera dove leggiamo la famosa affermazione Lo vedo ma non lo credo! Invitando Dedekind, studioso e della teoria dei numeri, a verificare il risultato ottenuto.
In conclusione possiamo affermare che Cantor ha dimostrato che esistono infiniti cardinali di infiniti, ovvero diverse categorie di infiniti definiti da lui numeri Transfiniti, Cantor era molto religioso e fece tale scelta per riservare solo a Dio il termine infinito.