Per geometria euclidea si intende la geometria che deriva più o meno direttamente dal compendio di matematica Gli Elementi composto da Euclide intornoal 300 a.c. ad Alessandria d’Egitto. La geometria presente nel trattato di Euclide tratta esclusivamente quella geometria che è possibile graficamente costruire con riga e compasso, benché già in epoca classica fossero note anche le così dette sezioni coniche http://slideplayer.it/slide/555581/1/images/4/La+costruzione+secondo+Menecmo.jpg delle quali si occupo anche Euclide in un’opera andata perduta. Euclide nella sua opera pose a fondamento della geometria cinque postulati e cinque nozioni comuni, non dimostrabili e da assumere intuitivamente come vere dalle quali far derivare tutte le dimostrazioni e i teoremi all’epoca conosciuti, per secoli questi postulati furono ritenuti veri e su di essi si fondò lo sviluppo della geometria nei secoli.
Per geometria euclidea si intende la geometria che deriva più o meno direttamente dal compendio di matematica Gli Elementi composto da Euclide intornoal 300 a.c. ad Alessandria d’Egitto. La geometria presente nel trattato di Euclide tratta esclusivamente quella geometria che è possibile graficamente costruire con riga e compasso, benché già in epoca classica fossero note anche le così dette sezioni coniche http://slideplayer.it/slide/555581/1/images/4/La+costruzione+secondo+Menecmo.jpg delle quali si occupo anche Euclide in un’opera andata perduta. Euclide nella sua opera pose a fondamento della geometria cinque postulati e cinque nozioni comuni, non dimostrabili e da assumere intuitivamente come vere dalle quali far derivare tutte le dimostrazioni e i teoremi all’epoca conosciuti, per secoli questi postulati furono ritenuti veri e su di essi si fondò lo sviluppo della geometria nei secoli.
-si possa tracciare una retta da un punto qualsiasi a un punto qualsiasi;
- si possa prolungare indefinitamente una linea retta;
- si possa descrivere un cerchio con un centro qualsiasi è un raggio qualsiasi;
- tutti gli angoli retti siano uguali;
- se una retta che interseca due altre rette forma dalla stessa parte angoli interni inferiori a due angoli retti, le due rette se estese indefinitamente, si incontrano da quella parte dove gli angoli sono inferiori a due angoli retti.
Quest'ultimo oggi è conosciuto da tutti gli studenti nella versione formulata da John Playfair (1748-1819), nota come assioma di playfair del 1795, che afferma:
dati una qualsiasi retta e un punto non appartenente a essa, è possibile tracciare per una e una sola retta parallela alla retta data.
https://image.isu.pub/131009165429-56b9c3e59627c66daf3ef872e4363511/jpg/page_53.jpg
Tuttavia i greci non si erano limitati a sviluppare la geometria di Euclide essi si cimentarono anche con la geometria sferica. Ciò nasceva dalla necessità di rispondere a problemi di tipo geografico e astronomico. I greci sapevano che la terra era sferica e addirittura Eratostene ne aveva misurata la grandezza con un piccolissimo errore rispetto alle dimension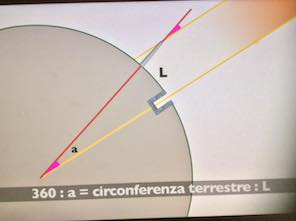 i effettive. Le motivazioni che li avevano condotti a ritenere la sferica la terra erano molteplici, per esempio che delle navi all’orizzonte si vedono prima gli alberi dello scafo https://4.bp.blogspot.com/-l3uwXDsn80k/WKqpRXemoDI/AAAAAAAACNs/JmZ_pItWe2QM-jV36hs-Lk2pMOcM74kUACK4B/s1600/3.png (che rimane sotto la line dell’orizzonte), sapevano che se si spostavano dalla Grecia all’alto Egitto (cioè cambiavano latitudine) mutavano le costellazioni visibili in cielo e ancora avevano notato che quando c’era un’eclissi parziale di luna l’ombra della terra proiettata sul nostro satellite era una curva. Oltre alla terra sferica, gli antichi affermavano che anche il cosmo, l’universo, fosse sferico e immaginavano che i corpi celesti si muovessero su delle sfere matematiche o fisiche che fossero. Fu questo che spinse gli antichi a costruire una “geometria sferica” che gli permettesse di descrivere la geografia terrestre e la fisica celeste.
i effettive. Le motivazioni che li avevano condotti a ritenere la sferica la terra erano molteplici, per esempio che delle navi all’orizzonte si vedono prima gli alberi dello scafo https://4.bp.blogspot.com/-l3uwXDsn80k/WKqpRXemoDI/AAAAAAAACNs/JmZ_pItWe2QM-jV36hs-Lk2pMOcM74kUACK4B/s1600/3.png (che rimane sotto la line dell’orizzonte), sapevano che se si spostavano dalla Grecia all’alto Egitto (cioè cambiavano latitudine) mutavano le costellazioni visibili in cielo e ancora avevano notato che quando c’era un’eclissi parziale di luna l’ombra della terra proiettata sul nostro satellite era una curva. Oltre alla terra sferica, gli antichi affermavano che anche il cosmo, l’universo, fosse sferico e immaginavano che i corpi celesti si muovessero su delle sfere matematiche o fisiche che fossero. Fu questo che spinse gli antichi a costruire una “geometria sferica” che gli permettesse di descrivere la geografia terrestre e la fisica celeste.
 Il
Il primo a fare progressi significativi nel campo della geometria sferica fu Menelao (70-140 d.c.) del quale ci è rimasta l’opera gli Sphaerica tra le alte cose per esempio individuo sulla superficie della sfera il corrispettivo del segmento sul piano euclideo.
primo a fare progressi significativi nel campo della geometria sferica fu Menelao (70-140 d.c.) del quale ci è rimasta l’opera gli Sphaerica tra le alte cose per esempio individuo sulla superficie della sfera il corrispettivo del segmento sul piano euclideo.
Rispetto alla geometria del piano euclideo individuarono diverse peculiarità in relazione agli assiomi euclidei, infatti, rispetto al primo postulato  si vede chiaramente in una sfera che per due punti passano infinite rette e non una sola retta. Per quanto riguarda il secondo postulato sulla superfice di una sfera i segmenti non possono essere estesi all’infinito come sul piano ma per così dire hanno un limite che è quello che corrisponde al cerchio massimo. Per quello che riguarda il terzo postulato
si vede chiaramente in una sfera che per due punti passano infinite rette e non una sola retta. Per quanto riguarda il secondo postulato sulla superfice di una sfera i segmenti non possono essere estesi all’infinito come sul piano ma per così dire hanno un limite che è quello che corrisponde al cerchio massimo. Per quello che riguarda il terzo postulato esso trova corrispondenza nelle due geometrie e rispetto alla geometria sferica individua quelli che noi chiamiamo paralleli. Il quarto postulato è anch’esso invariante. Il quinto postulato si vede chiaramente che non è valido sulla superfice di una sfera perché tutte le “rette” si incontrano in almeno d
esso trova corrispondenza nelle due geometrie e rispetto alla geometria sferica individua quelli che noi chiamiamo paralleli. Il quarto postulato è anch’esso invariante. Il quinto postulato si vede chiaramente che non è valido sulla superfice di una sfera perché tutte le “rette” si incontrano in almeno d ue punti e non esistono pertanto rete parallele.
ue punti e non esistono pertanto rete parallele.
Malgrado questi studi in epoca antica non si considerò questa una vera e propria geometria, ma una tecnica per risolvere particolari problemi, così come si era fatto a proposito delle sezioni coniche.
A partire dalla rivoluzione scientifica si iniziò a studiare, sempre più approfonditamente la natura delle curve che non si costruivano con il compasso. Va ricordato che proprio nei primi anni del ‘600 Keplero aveva mostrato che le orbite planetarie erano delle ellissi e non dei cerchi. Il primo a cimentarsi nell’analisi matematica delle curve prodotte dalle coniche fu Cartesio con la sua geometria analitica e a seguire Newton (per onor del vero questi sono solo quelli più famosi). Da questi studi nacque lo studio di figure particolari come la pseudo sfera che a differenza della sfera si costruisce a partire dalla trattrice, curva che rimanda all’iperbole, intorno al suo asintoto. Rispetto a figure come queste i matematici si chiedevano se si potesse usare la geometria euclidea oppure quella sferica con cui aveva alcune cose in comune ma non tutte a partire della curvatura, infatti, mentre la curvatura di una sfera e positiva ovvero concava quella della pseudo sfera e negativa ovvero convessa.
non dei cerchi. Il primo a cimentarsi nell’analisi matematica delle curve prodotte dalle coniche fu Cartesio con la sua geometria analitica e a seguire Newton (per onor del vero questi sono solo quelli più famosi). Da questi studi nacque lo studio di figure particolari come la pseudo sfera che a differenza della sfera si costruisce a partire dalla trattrice, curva che rimanda all’iperbole, intorno al suo asintoto. Rispetto a figure come queste i matematici si chiedevano se si potesse usare la geometria euclidea oppure quella sferica con cui aveva alcune cose in comune ma non tutte a partire della curvatura, infatti, mentre la curvatura di una sfera e positiva ovvero concava quella della pseudo sfera e negativa ovvero convessa.
Tuttavia la storia della genesi delle geometrie non euclidee non trova i suoi veri fondamenti in questi studi, ma dai dubbi riguardo la legittimità del quinto postulato euclideo. Euclide stesso aveva mostrato diffidenza verso questo postulato che sembra più un teorema che non una verità intuitiva, tuttavia era stato costretto ad inserirlo nella sua opera perché fondamentale nella dimostrazione di numerosi teoremi in primis il celebre Teorema di Pitagora. Fin dall’opera di Euclide diversi matematici si cimentarono nel tentativo di ricavare per via dimostrativa il quinto postulato dagli altri quattro senza però riuscirvi.
Malgrado gli insuccessi alcuni di questi tentativi furono determinanti per lo sviluppo delle geometrie non euclidee. Di particolare rilevanza sono gli studi del gesuita Girolamo Saccheri (1667-1733) e quelli di Johann Heinrich Lambert (1728-1777).
 Saccheri, matematico dell’università di Pavia, scrisse un trattato Euclide ab omni naevo vindicatus (Euclide liberato da ogni macchia), dove tentò di dimostrare il quinto postulato avvalendosi della dimostrazione per assurdo.
Saccheri, matematico dell’università di Pavia, scrisse un trattato Euclide ab omni naevo vindicatus (Euclide liberato da ogni macchia), dove tentò di dimostrare il quinto postulato avvalendosi della dimostrazione per assurdo.
Da principio costruì una figura. Parti da un segmento AB e tracciò due perpendicolari ai suoi estremi AD e BC (perpendicolari dunque formando angoli retti di 90° con il segamento AB), tracciò poi il segmento che univa le due perpendicolari e si chiese se i due angoli che ne risultavano fo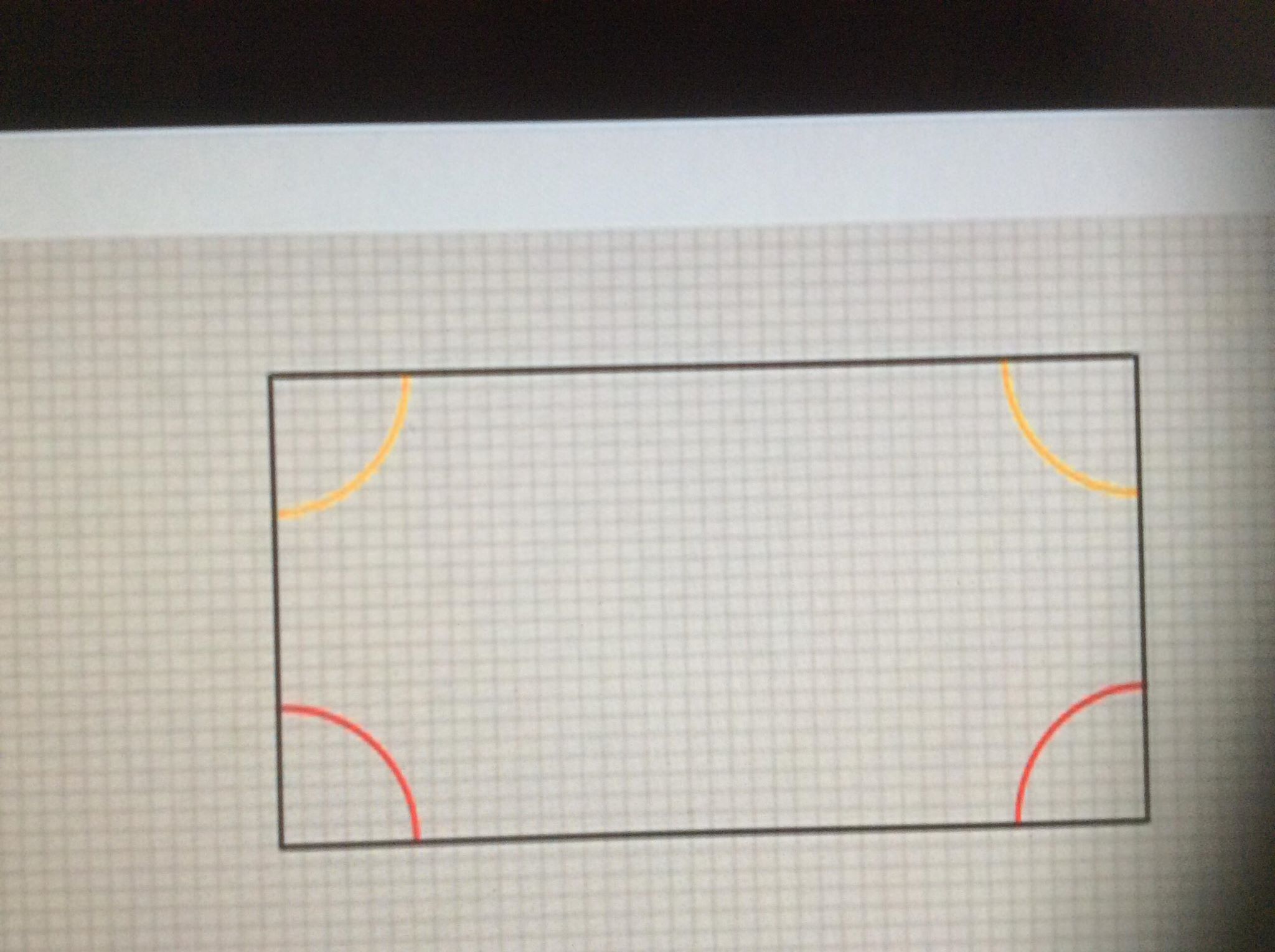 ssero essi stessi retti, cioè di 90°. Come si evince dalla figura le possibilità che possiamo prendere in esame a proposito degli angoli che abbiamo ricavato congiungendo i due segmenti sono solo tre, la prima è che essi siano come gli angoli della base di 90° cioè retti, la seconda che siano acuti ovvero minori <90° la terza è che siano ottusi ovvero maggiori >90°.
ssero essi stessi retti, cioè di 90°. Come si evince dalla figura le possibilità che possiamo prendere in esame a proposito degli angoli che abbiamo ricavato congiungendo i due segmenti sono solo tre, la prima è che essi siano come gli angoli della base di 90° cioè retti, la seconda che siano acuti ovvero minori <90° la terza è che siano ottusi ovvero maggiori >90°.
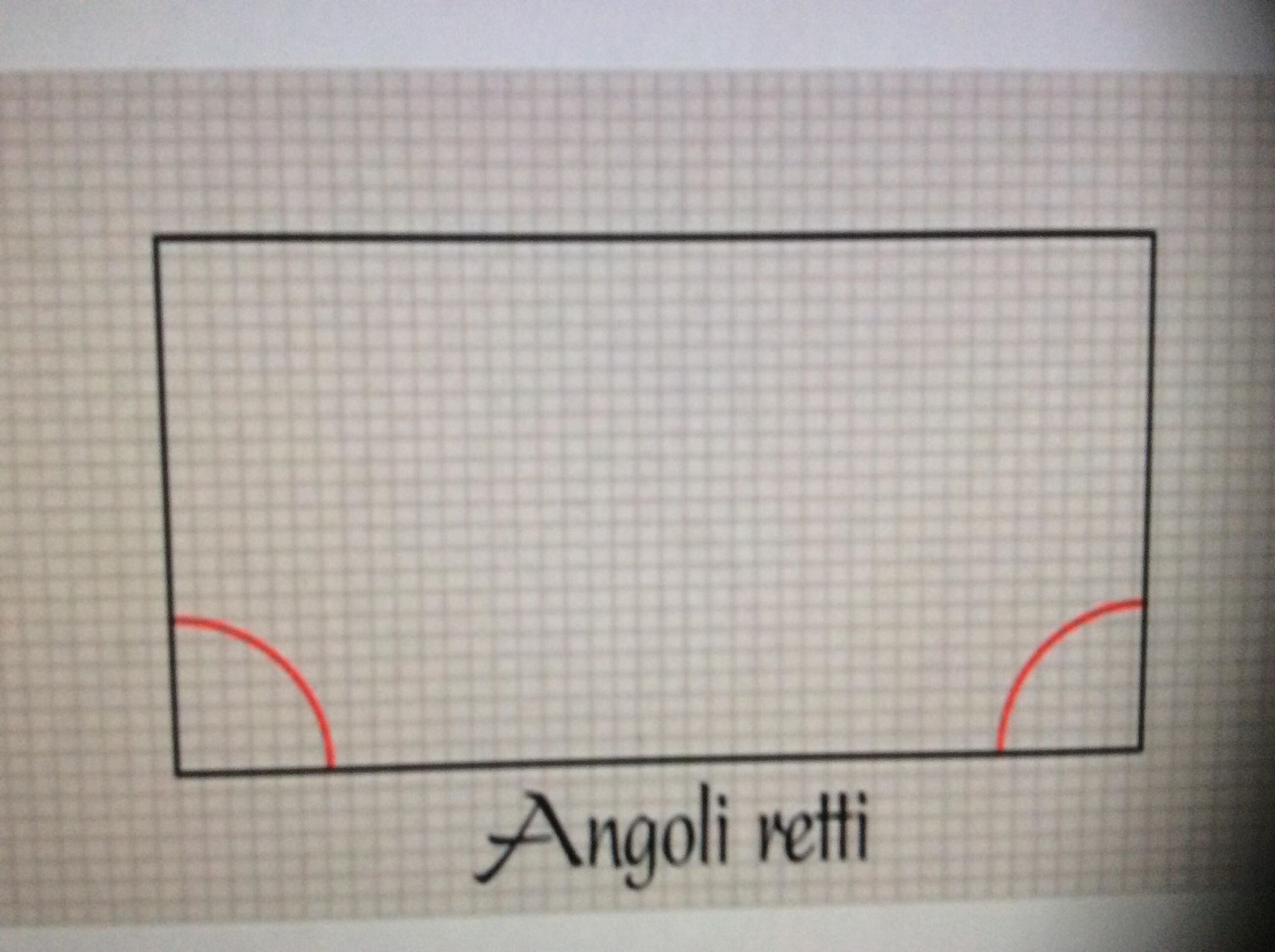
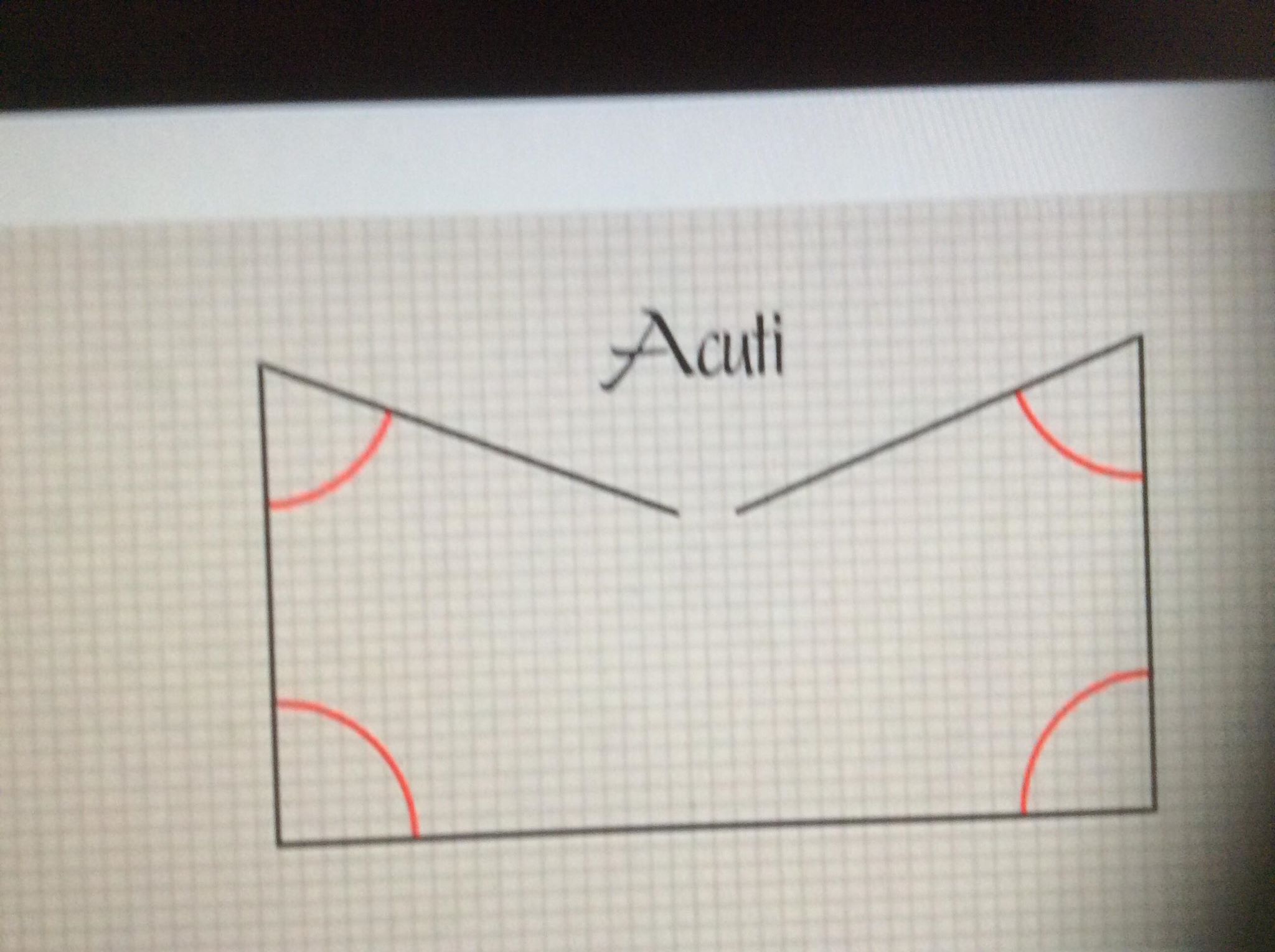
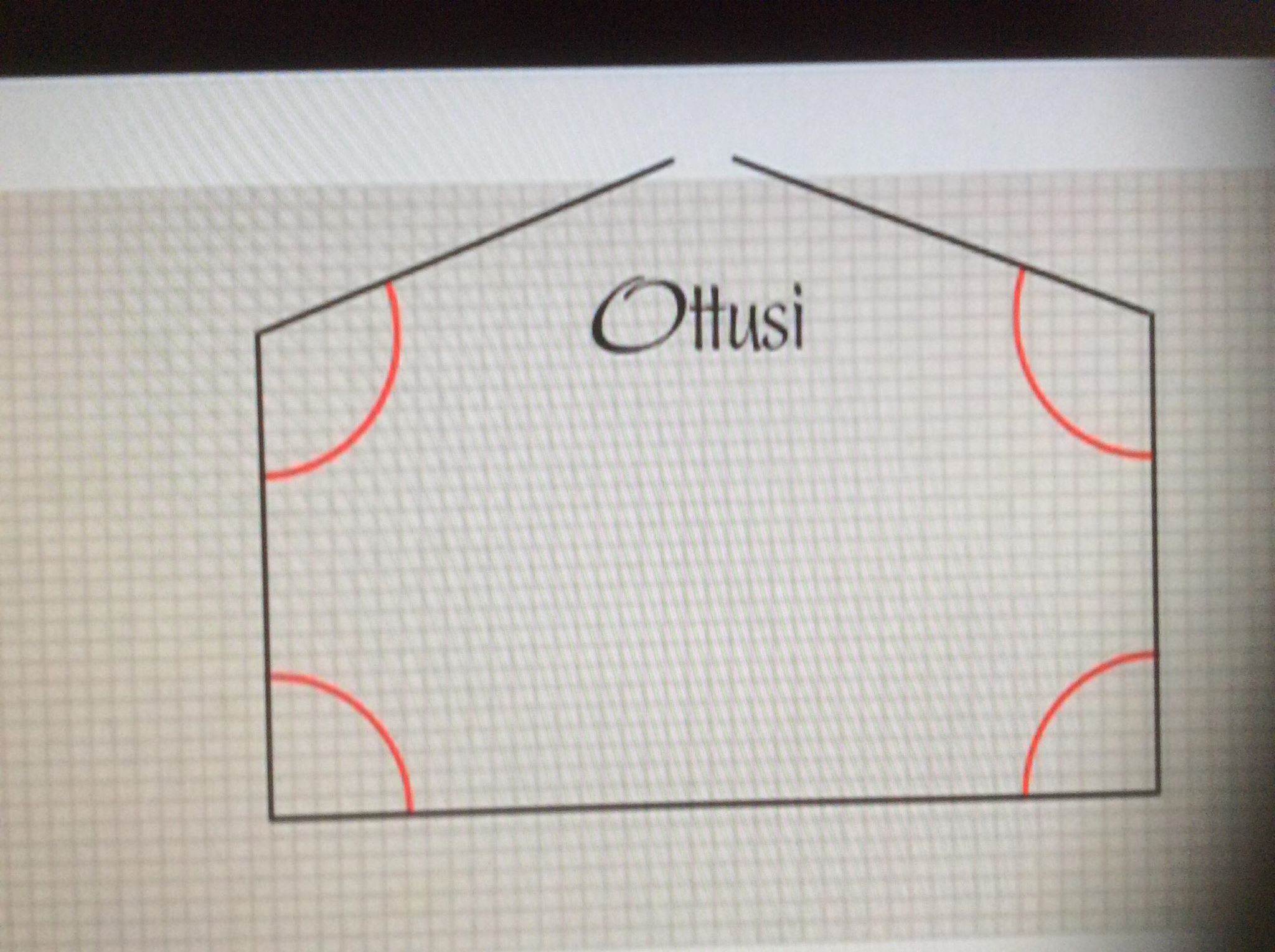
Per quanto riguarda l’ipotesi degli angoli ottusi Saccheri la confutò assumendo per vero che una retta dovesse avere per forza lunghezza infinita, cosa che tuttavia non vale nella geometria sferica e non da origine a contraddizioni; per quanto riguarda l’ipotesi degli angoli acuti egli derivò diversi teoremi ma non riuscì a trovare una contraddizione matematica che la invalidasse dunque attraverso un ragionamento, filosofico più che matematico, sentenziò che l’ipotesi dell’angolo acuto è assolutamente falsa; perchè essa ripugna alla natura della linea retta. Affermata l’impossibilità di due delle tre opzioni, non rimaneva che sostenere quella che vuole i due angoli che abbiamo formato essere retti ovvero uguali a 90° il che dimostrerebbe il quinto postulato di Euclide. Per onor del vero Saccheri stesso era ben consapevole del fallimento della sua opera che infatti vide la luce solo l’anno della sua morte, e non avendo mai riconosciuto la validità dei teoremi che scaturivano dall’ipotesi dell’angolo acuto non gli poté essere riconosciuto nemmeno postumo il merito di aver avviato gli studi di geometria iperbolica.
Diversamente Lambert https://www.orthotes.com/wp-content/uploads/2017/02/jhlambert.jpg in Die Theorie der Parallellinien , pur non riuscendo come Saccheri ha dimostrare il quinto postulato, non negò del tutto la possibilità dell’esistenza di una geometria coerente non euclidea. Egli affermo nella sua opera:
Mi sembra notevole che l’ipotesi dell’angolo ottuso sia valida se invece di un tringolo piano consideriamo un triangolo sferico, poiché la somma dei suoi angoli è maggiore di 180°

Riprendendo il lavoro di Menelao sulla geometria sferica. Poi Lambert immaginò che l’ipotesi dell’angolo acuto poteva corrispondere a una geometria su una superficie di tipo nuovo, come quella di una sfera di raggio immaginario. Questa è una considerazione molto complessa da immaginare perché infatti è necessario operare su una sfera con uno pseudoraggio cioè un raggio che sia la radice quadrata di un numero negativo, così facendo però avviò gli studi sulla curvatura negativa (che poi sarebbe quella che oggi chiamiamo geometria iperbolica). Questo lo portò a creare alcuni dei primissimi teoremi di geometria iperbolica in particolare quello che permette di ricavare l’area di un triangolo su una superficie a curvatura negativa conoscendo l’ampiezza dei suoi angoli π-(α+β+γ)=CΔ. https://encrypted-tbn0.gstatic.com/images?q=tbn%3AANd9GcQwCDxY_TUhIlZwA5rSW4H6jZ9L6ydHqFlqBavyYuUL36teykwU&usqp=CAU Anche se Lambert non viene riconosciuto come l’inventore della geometria iperbolica sappiamo per certo che fu determinante per gli scopritori delle geometrie non euclidee.