 La geometria scoperta da Nikolai Lobachevsky (1793-1856) e da Jànos Bolyai (1812-1860) è la prima Geometria non Euclidea ed è conosciuta come Geometria iperbolica, in Greco "iperbole" significa "eccesso" https://www.youmath.it/images/stories/formulari/geometria-analitica/iperbole-nel-piano-cartesiano.png e in tale geometria il numero delle rette parallele ad una retta data e passanti per un punto fissato è in "eccesso" rispetto a quello della Geometria Euclidea.
La geometria scoperta da Nikolai Lobachevsky (1793-1856) e da Jànos Bolyai (1812-1860) è la prima Geometria non Euclidea ed è conosciuta come Geometria iperbolica, in Greco "iperbole" significa "eccesso" https://www.youmath.it/images/stories/formulari/geometria-analitica/iperbole-nel-piano-cartesiano.png e in tale geometria il numero delle rette parallele ad una retta data e passanti per un punto fissato è in "eccesso" rispetto a quello della Geometria Euclidea.
 Nikolai Lobachevsky (1793-1856) era figlio di un modesto funzionario governativo russo, rimasto orfano a sette anni, nonostante le difficoltà economiche della famiglia, Nicolai fu mandato a studiare all’università del Kazan. Qui divenne allievo del matematico tedesco J.M. Bartels che prima di trasferirsi in Kazan aveva insegnato a Gottinga e aveva avuto tra i suoi allievi anche Gauss. Lobachevsky fece una carriera rapidissima a 21 anni divenne professore presso l’’università del Kazan e a nel 1827 ne divenne Rettore https://rusiacondaleko.com/wp-content/uploads/2019/06/1qqqq.jpeg. La sua opera principale fu i Nuovi elementi di geometria del 1835. All’Università del Kazan insegnò e studiò tutta vita fino alla morte sopraggiunta nel 1856. Purtroppo gli ultimi anni della sua vita furono amareggiati dall’avversione del matematico Mijail Ostrogradskij, il quale si opponeva a qualsiasi critica alla geometria euclidea, e che riuscì a farlo destituire dal ruolo di Rettore nel 1846. Progressivamente Lobachevsky perse anche la vista e fu costretto a dettare le sue ultime opere.
Nikolai Lobachevsky (1793-1856) era figlio di un modesto funzionario governativo russo, rimasto orfano a sette anni, nonostante le difficoltà economiche della famiglia, Nicolai fu mandato a studiare all’università del Kazan. Qui divenne allievo del matematico tedesco J.M. Bartels che prima di trasferirsi in Kazan aveva insegnato a Gottinga e aveva avuto tra i suoi allievi anche Gauss. Lobachevsky fece una carriera rapidissima a 21 anni divenne professore presso l’’università del Kazan e a nel 1827 ne divenne Rettore https://rusiacondaleko.com/wp-content/uploads/2019/06/1qqqq.jpeg. La sua opera principale fu i Nuovi elementi di geometria del 1835. All’Università del Kazan insegnò e studiò tutta vita fino alla morte sopraggiunta nel 1856. Purtroppo gli ultimi anni della sua vita furono amareggiati dall’avversione del matematico Mijail Ostrogradskij, il quale si opponeva a qualsiasi critica alla geometria euclidea, e che riuscì a farlo destituire dal ruolo di Rettore nel 1846. Progressivamente Lobachevsky perse anche la vista e fu costretto a dettare le sue ultime opere.
Lobachevsky può essere considerato il “Copernico della geometria”. La concezione rivoluzionaria del matematico Kazaco non fu una illuminazione improvvisa, ma il frutto di anni di studi. Ancora nel 1823 Lobachevsky rifletteva sull’assioma delle parallele, ovvero il quinto postulato euclideo, e solo nel 1826 inizio a enunciare i primi teoremi. Tra il 1826 e il 1829 dichiarò l’impossibilità di dimostrare il quinto postulato euclideo e nel 1829 nel saggio Sui principi della geometria pubblicato sulla Gazzetta del Kazan affermò l’esistenza di una geometria che si fondava sull’idea che per un punto C che giace al di fuori della retta AB si può tracciare sullo stesso piano molteplici rette che non incontrino il segmento AB, cioè negando l’assioma delle parallele.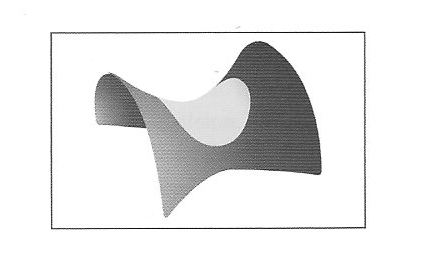
Contemporaneamente a Lobachevsky giunse a tali conclusioni anche l’ungherese Jànos Bolyai (1812-1860) figlio del matematico Farkas Bolyai https://c8.alamy.com/compit/ppmtgj/bolyai-farkas-ppmtgj.jpg amico di Gauss. Ufficiale di cavalleria di professione si inizio a occupare continuativamente di matematica dopo aver frequentato i corsi all’università di Ingegneria militare a Vienna. Bolyai non pubblicò vere e proprie opere durante la sua vita, ma troviamo le sue idee di geometria non e uclidea in un Appendice ad un testo del padre. Inoltre dopo la sua morte furono rinvenute 20.000 pagine di manoscritti sull’argomento. Egli aveva studiato le conseguenze legate al teorema delle parallele con un intensità e tenacia senza pari tanto che il padre scrisse in una lettera a Gauss che il figlio era in preda ad una vera e propria ossessione. Bolyai dopo essersi reso conto dell’impossibilità di dimostrare l’assioma euclideo sviluppò quella che egli battezzò “Scienza assoluta” partendo dall’ipotesi che per un punto esterno ad una retta si possono tracciare nello stesso piano, infinite rette parallele alla retta data.
uclidea in un Appendice ad un testo del padre. Inoltre dopo la sua morte furono rinvenute 20.000 pagine di manoscritti sull’argomento. Egli aveva studiato le conseguenze legate al teorema delle parallele con un intensità e tenacia senza pari tanto che il padre scrisse in una lettera a Gauss che il figlio era in preda ad una vera e propria ossessione. Bolyai dopo essersi reso conto dell’impossibilità di dimostrare l’assioma euclideo sviluppò quella che egli battezzò “Scienza assoluta” partendo dall’ipotesi che per un punto esterno ad una retta si possono tracciare nello stesso piano, infinite rette parallele alla retta data.
Bernhard Georg Friedrich Riemann (1826-1866) rappresenta il terzo personaggio grazie al quale si svilupparono le geometrie non euclidee. Il nome di Riemann è indissolubilmente legato da un lato alla geometria che ha trovato applicazione nella teoria della relatività di Einstein e dall’altro alla congettura di Riemann riguardo i numeri primi.
 Riemann nacque il 17 settembre del 1826 in un villaggio della bassa Sassonia come secondo di sei figli di un pastore luterano. A causa delle ristrettezze economiche della famiglia fino all’età di quattordici anni dovette studiare da autodidatta e solo nel 1840 poté entrare nel liceo di Hannover. Dopo nel 1846 dopo aver abbandonato gli studi di teologia a Gottinga, ai quali era stato avviato dal padre, iniziò a seguire i corsi di matematica di Friedrich Gauss. Proseguì gli studi a Berlino, e divenne poi assistente di fisica a Gottinga, dopo essere stato nominato professore nel 1857, dal 1859 occupo la cattedra che un tempo era stata quella Gauss. I principali studi di Riemann riguardano la teoria dei numeri e la geometria. Malato di tubercolosi venne a curarsi in Italia dove si spense il 20 giugno del 1866 a Selasca nella provincia di Verbania sul Lago maggiore https://www.immobiliareborsetta.com/images/bb.jpeg dove se pur non è più presente la sua tomba, andata distrutta, possiamo ancora ritrovare la lapide che ne onora la memoria. https://upload.wikimedia.org/wikipedia/commons/thumb/0/01/2009_11_riemann_008.jpg/1200px-2009_11_riemann_008.jpg
Riemann nacque il 17 settembre del 1826 in un villaggio della bassa Sassonia come secondo di sei figli di un pastore luterano. A causa delle ristrettezze economiche della famiglia fino all’età di quattordici anni dovette studiare da autodidatta e solo nel 1840 poté entrare nel liceo di Hannover. Dopo nel 1846 dopo aver abbandonato gli studi di teologia a Gottinga, ai quali era stato avviato dal padre, iniziò a seguire i corsi di matematica di Friedrich Gauss. Proseguì gli studi a Berlino, e divenne poi assistente di fisica a Gottinga, dopo essere stato nominato professore nel 1857, dal 1859 occupo la cattedra che un tempo era stata quella Gauss. I principali studi di Riemann riguardano la teoria dei numeri e la geometria. Malato di tubercolosi venne a curarsi in Italia dove si spense il 20 giugno del 1866 a Selasca nella provincia di Verbania sul Lago maggiore https://www.immobiliareborsetta.com/images/bb.jpeg dove se pur non è più presente la sua tomba, andata distrutta, possiamo ancora ritrovare la lapide che ne onora la memoria. https://upload.wikimedia.org/wikipedia/commons/thumb/0/01/2009_11_riemann_008.jpg/1200px-2009_11_riemann_008.jpg
Per quanto riguarda il primo dei temi a cui è legato Riemann, ovvero rispetto alla distribuzione dei numeri primi nell’insieme dei numeri naturali (ovvero gli interi 0,1,2,3,4,5….), possiamo partire dalla definizione di numero primo, che tutti abbiamo imparato a scuola, ovvero è detto primo il numero che ha come divisori soltanto 1 e se stesso (ad esempio 2,3,5,7…). Il primo a dimostrare che la quantità dei numeri primi è illimitata fu proprio Euclide https://image3.slideserve.com/5816473/slide1-n.jpg attraverso una dimostrazione molto semplice: si nota facilmente che se prendiamo i primi tre numeri primi 2, 3 e 5 e li moltiplichiamo tra loro otteniamo un numero 30 che sarà sicuramente divisibile per 2, per 3 e per 5, ma se a tal numero sommiamo +1 otterremmo un numero, che è appunto 31, che se diviso avrà sempre come resto 1 ovvero non ha divisori se non 1 e se stesso. Questo ci fa notare che esiste una regola molto semplice che ci mostra che moltiplicando tra loro i numeri primi noti e sommando ad essi +1 si ottiene sempre un nuovo numero primo e così via senza limiti.
La dimostrazione può essere fatta ragionando per assurdo:
supponiamo per assurdo che il numero dei numeri primi sia finito, lì indichiamo con p1, p2, p3…pn. Consideriamo il numero p= p1· p2· p3·….· pn+1. Abbiamo solo due possibilità se p non ha divisori ovvero è primo si ha una contraddizione perché abbiamo trovato un nuovo numero primo, se p non è primo allora deve esistere un numero q che lo divide che sia primo ma questo non può essere rintracciato tra p1, p2, p3…pn dato che se lo dividiamo per questi numeri otterremmo sempre il resto di 1, quindi anche in questo caso si ha una contraddizione perché dovrebbe comunque esistere un ulteriore numero primo in aggiunta a quelli noti. https://www-dimat.unipv.it/~cornalba/lezioni/primi/euclid.jpg
Questa dimostrazione ci dice però solo che i numeri primi sono infiniti, ma non quando e ogni quanto incontreremo il prossimo numero primo nello scorrere l’insieme dei numeri naturali. L’ipotesi z di Riemann afferma che man mano che si scorre l’insieme dei numeri naturali i numeri primi si diradano, ma non con un andamento casuale, ma attraverso un intervallo che segue una funzione ricorrente. http://www.andreaminini.org/data/andreamininiorg/teorema-numeri-primi-esempio.gif Malgrado questa congettura possa essere percepita e intuita né Riemann né nessun altro è riuscito ad oggi a dimostrala. Tale congettura è anche alla base degli studi compiuti dal matematico statunitense John Fobes Nasch https://lamenteemeravigliosa.it/wp-content/uploads/2017/11/John-nash.jpg?width=1200&enable=upscale premio Nobel nel 1994 per l’economia per la sua teoria dei giochi a somma non zero, celebre per il film a lui dedicato A beautiful mind dove si racconta della sua incredibile battaglia interiore per sconfiggere la schizofrenia. Nasch è purtroppo scomparso il 23 maggio 2015 in un incidente stradale.
Per quanto riguarda la geometria l’idea di Riemann, costruita sulla definizione di curvatura compiuta da Gauss, è quella di porre oltre all’ipotesi di Lobachevsky e Bolyai, anche quella in cui data una retta AB ed un punto P non appartenente alla retta, non esistono rette passati per il punto P che siano parallele alla retta AB. Da questo assunto nasce la geometria ellittica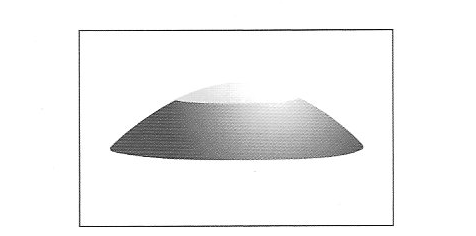
Le conseguenze di queste due prospettiva hanno valenza sia sul piano geometrico, fisico e su quello filosofico. Per quanto riguarda il piano filosofico veniva meno l’idea kantiana che la geometria fosse il frutto dell’applicazione della forma pura di spazio euclideo presente nella sensibilità umana all’esperienza, e si veniva così a riproporre il tema dei fondamenti della geometria accanto a quello dei fondamenti dell’aritmetica. Dal punto di vista della fisica questi studi contribuiranno alla nuova idea di spazio-tempo di Hermann Minkowski e Albert Einstein. http://www.fisicauniversale.com/wp/wp-content/uploads/2019/01/cono-di-luce-1-768x734.jpg Per quanto riguarda lo sviluppo della geometria che ci interessa trattare la conseguenza immediata è che la geometria euclidea non è altro che un caso particolare della geometria e che le geometrie non euclidee sono infinite nel senso che dipendendo dalla curvatura (positiva o negativa) in base ad essa si possono costruire infiniti modelli di spazio geometrico.
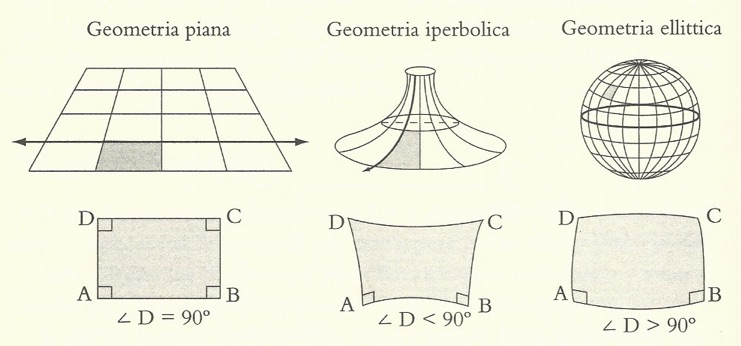
Classificando in tre grandi gruppi le diverse geometrie possiamo distinguerle come segue:
Nella geometria euclidea vale il quinto postulato euclideo. In quella iperbolica a curvatura negativa vale l’assunto che data una retta e un punto esterno ad essa vi passano infinite parallele. Nella geometria ellittica infine non vi sono rette parallele.
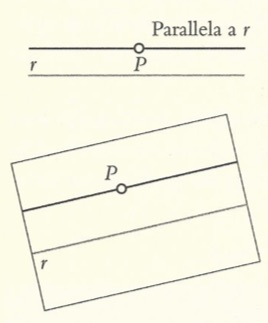
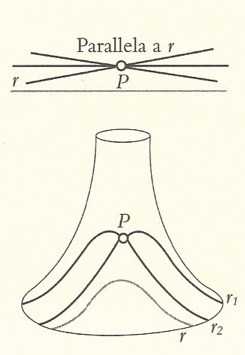
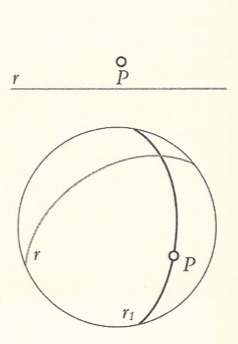
Proviamo a vedere alcune conseguenze di ciò. Nella geometria Euclidea le rette parallele hanno tra loro tutti i punti equidistanti, nella geometria iperbolica no. Nella geometria euclidea e solo in quella vale il teorema di Pitagora, nelle altre no. Solo nella geometria euclidea la somma degli angoli interni di un triangolo è pari a 180°. In quella iperbolica la somma degli angoli interni è (minore) <180°, in quella ellittica è (maggiore) >180°
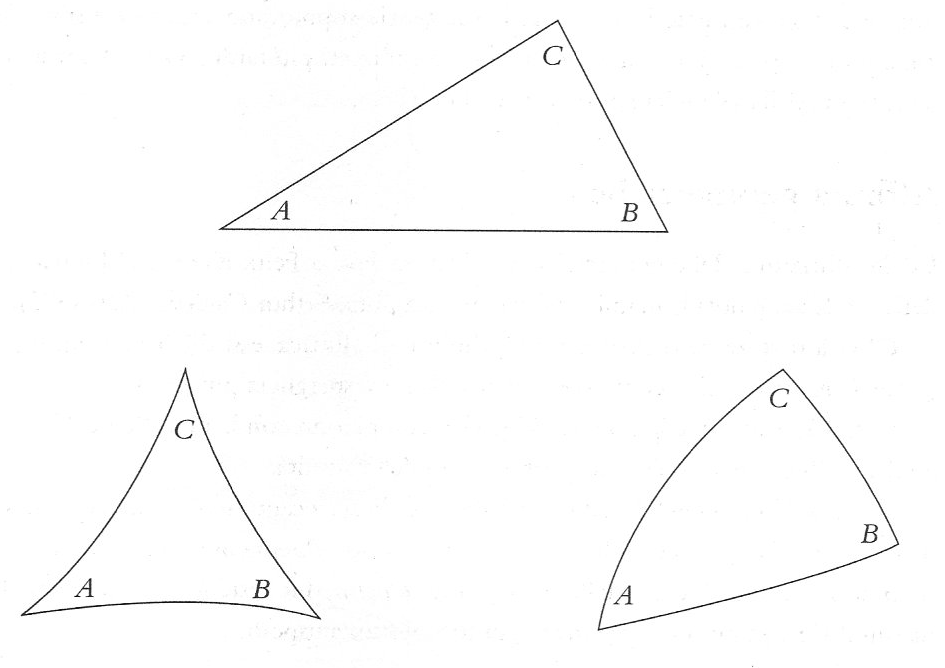
Nella geometria iperbolica tanto più un’area di un triangolo è ampia tanto minore sarà la somma degli angoli interni, così che possono esistere triangoli uguali ma non simili. Nella geometrie non euclidee scompaiono figure come i rettangoli.
| Geometria | autore | Parallele ad un punto esterno | somma degli angoli di un triangolo | Le rette sono |
| piana | Euclide | una | = 180° | infinite |
| iperbolica | Lobachevsky-Bolyai | infinite | < 180° | infinite |
| ellittica | Riemann | nessuna | > 180° | finite |