 Apollonio insieme a Ipparco e Tolomeo rappresentano il tentativo più significativo nell’antichità di rispondere alla celebre domanda di Platone narrata da Simplicio
Apollonio insieme a Ipparco e Tolomeo rappresentano il tentativo più significativo nell’antichità di rispondere alla celebre domanda di Platone narrata da Simplicio
Platone ammette in generale che i corpi celesti si muovono di moto circolare, uniforme e costantemente regolare; egli allora pone ai matematici questo problema: quali sono i movimenti circolari, uniformi e perfettamente regolari che conviene prendere come ipotesi per poter salvare le apparenze presentate dai pianeti? (Simplicio, Commento al De Caelo di Aristotele).
Va ricordato che Platone come in generale gli antichi ben vedevano che i moti non erano perfettamente circolari, ed è proprio per questo che viene usata l’espressione “salvare i fenomeni”, solo Aristotele tra i grandi del passato ebbe l’ardire di costruire un modello fisico assoluto (e tutti sappiamo che è andata a finire), a Platone e ai grandi matematici dell’antichità bastava avere un modello matematico e relativo che prevedesse i fenomeni in modo verosimile (in questo mostrando di essere alla pari degli scienziati contemporanei); in particolare gli astronomi avevano dovuto risolvere il problema delle irregolarità dei moti planetari e soprattutto del moto così detto "retrogrado" dovuto alla non perfetta circolarità delle orbite e al fatto che non è la Terra al centro del mondo.
Va poi ricordato che il cerchio, la sfera e il moto circolare uniforme erano gli unici strumenti geometrici compiutamente dominati dagli antichi, pertanto una teoria che aveva l’obiettivo di prevedere e calcolare i moti celesti non poteva prescindere da una descrizione tramite moti circolari uniformi. https://www.unionegeometri.com/wp-content/uploads/2021/11/geometria-euclidea-e-non-euclidea-1024x512.png Infatti lo studio delle coniche, elissi, iperbole e parabole avrebbe trovato compimento solo con i matematici moderni Keplero, Cartesio e Newton.
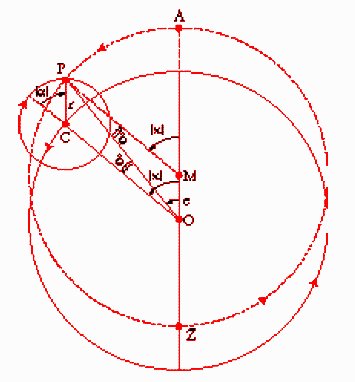
 Apollonio di Perga pare sia vissuto tra il 262 a.c. e il 190 a.c. e che come Archimede si sia formato ad Alessandria e li abbia probabilmente anche tenuto delle lezioni. Egli è l’alter ego, se così si può dire, di Euclide, infatti esso è soprattutto famoso per la sua opera sulle sezioni coniche (oltre che per il suo contributo all’astronomia di cui si dirà in seguito), ma va subito precisato che la sua opera si avvale dei contributi proprio di alcuni scritti di Euclide sull’argomento che invece sono andati perduti. Ma cosa sono le sezioni coniche? Sono appunto sezioni di coni che generano ellisse, parabola ed iperbole queste pur essendo state già studiate sia da Euclide che da Archimede (e dal platonico Menecmo http://slideplayer.it/slide/555581/1/images/4/La+costruzione+secondo+Menecmo.jpg) furono sistemate compiutamente nell’opera di Apollonio egli «fu il primo a fondare la teoria di tutte e tre le sezioni coniche sulle sezioni di un unico cono circolare, retto o obliquo»https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcQDod1l3mJFD7ojNi6g5_CUz2BOJm5H_aWecJMyQrdTyOgSFW2N&s. L’opera era composta da otto libri, di cui ci rimangono in originale i primi quattro, in una versione araba altri tre, e l’ottavo è stato ricostruito dal grande astronomo, Halley (l’amico di Newton e l’ispiratore dei Principia), grazie ai lasciti del matematico Pappo. Apollonio è considerato il vero padre adottivo dei moti eccentrici https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcRnw-CZESpZRv9E5xDBxVjCLkDVzMUYtGEorZ-hPW6o2V51j4RK&s (adottivo perchè non sono stati introdotti da lui; questi erano già conosciuti al tempo di Aristarco) e degli epicicli, in particolare, egli perfezionò la teoria esistente introducendo il concetto di “eccentrico mobile”. https://upload.wikimedia.org/wikipedia/commons/thumb/4/42/Schiaparelli_141.png/450px-Schiaparelli_141.png Quest’ultima teoria sostanza la variazione consiste nel porre il centro dell’eccentrico non in un luogo qualunque, più o meno vicino alla Terra, ma sulla linea retta che va dalla Terra al Sole, che, come si è già anticipato, fa sì che il centro dell’eccentrico disegni a sua volta un’orbita attorno alla Terra, dunque un centro mobile. Nel suo sistema Venere e Mercurio si muovevano su un eccentrico e il loro centro era posizionato in modo che la loro orbita fosse sempre esterna alla Terra, e intrecciasse l’orbita del Sole, che invece si muoveva in un cerchio concentrico assieme alla Luna; differentemente i pianeti esterni si muovevano sempre con moti eccentrici; avevano il loro centro posizionato in un punto della retta Sole/Terra, tale che la loro orbita fosse sempre esterna sia alla Terra sia all’orbita del Sole e della Luna. Tale teoria, rispetto a quella delle sfere omocentriche di Eudosso, dava molte più ragioni dei moti irregolari dei pianeti.
Apollonio di Perga pare sia vissuto tra il 262 a.c. e il 190 a.c. e che come Archimede si sia formato ad Alessandria e li abbia probabilmente anche tenuto delle lezioni. Egli è l’alter ego, se così si può dire, di Euclide, infatti esso è soprattutto famoso per la sua opera sulle sezioni coniche (oltre che per il suo contributo all’astronomia di cui si dirà in seguito), ma va subito precisato che la sua opera si avvale dei contributi proprio di alcuni scritti di Euclide sull’argomento che invece sono andati perduti. Ma cosa sono le sezioni coniche? Sono appunto sezioni di coni che generano ellisse, parabola ed iperbole queste pur essendo state già studiate sia da Euclide che da Archimede (e dal platonico Menecmo http://slideplayer.it/slide/555581/1/images/4/La+costruzione+secondo+Menecmo.jpg) furono sistemate compiutamente nell’opera di Apollonio egli «fu il primo a fondare la teoria di tutte e tre le sezioni coniche sulle sezioni di un unico cono circolare, retto o obliquo»https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcQDod1l3mJFD7ojNi6g5_CUz2BOJm5H_aWecJMyQrdTyOgSFW2N&s. L’opera era composta da otto libri, di cui ci rimangono in originale i primi quattro, in una versione araba altri tre, e l’ottavo è stato ricostruito dal grande astronomo, Halley (l’amico di Newton e l’ispiratore dei Principia), grazie ai lasciti del matematico Pappo. Apollonio è considerato il vero padre adottivo dei moti eccentrici https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcRnw-CZESpZRv9E5xDBxVjCLkDVzMUYtGEorZ-hPW6o2V51j4RK&s (adottivo perchè non sono stati introdotti da lui; questi erano già conosciuti al tempo di Aristarco) e degli epicicli, in particolare, egli perfezionò la teoria esistente introducendo il concetto di “eccentrico mobile”. https://upload.wikimedia.org/wikipedia/commons/thumb/4/42/Schiaparelli_141.png/450px-Schiaparelli_141.png Quest’ultima teoria sostanza la variazione consiste nel porre il centro dell’eccentrico non in un luogo qualunque, più o meno vicino alla Terra, ma sulla linea retta che va dalla Terra al Sole, che, come si è già anticipato, fa sì che il centro dell’eccentrico disegni a sua volta un’orbita attorno alla Terra, dunque un centro mobile. Nel suo sistema Venere e Mercurio si muovevano su un eccentrico e il loro centro era posizionato in modo che la loro orbita fosse sempre esterna alla Terra, e intrecciasse l’orbita del Sole, che invece si muoveva in un cerchio concentrico assieme alla Luna; differentemente i pianeti esterni si muovevano sempre con moti eccentrici; avevano il loro centro posizionato in un punto della retta Sole/Terra, tale che la loro orbita fosse sempre esterna sia alla Terra sia all’orbita del Sole e della Luna. Tale teoria, rispetto a quella delle sfere omocentriche di Eudosso, dava molte più ragioni dei moti irregolari dei pianeti.