Lo sviluppo dell’astronomia, nella scuola di Alessandria, tocca il suo apice con Claudio Tolomeo. Di Tolomeo, da non confondere con i re egizi, non si conosce con precisione né luogo né data di nascita si suppone sia nato o ad Alessandria stessa oppure a Tolemaide o a Pelusio, sappiamo invece che egli operò nella prima metà del II secolo d.c., fu influenzato dalla filosofia platonica e stoica e, naturalmente, dalla dottrina pitagorica intorno ai numeri.
Di solito nella cultura Occidentale viene utilizzata l’espressione impropria di sistema astronomico aristotelico-tolemaico; innegabilmente i due sistemi astronomici condividono la stessa concezione cosmologica geocentrica con la terra immobile e al centro delle sfere celesti. Tuttavia differiscono profondamente sia sul tipo di moto che per Tolomeo è eccentrico https://toolazytobeatrekkie.files.wordpress.com/2014/11/img_0143.gif?w=400 mentre per Aristotele è concentrico e ripreso dal modello di Eudosso https://www.geogebra.org/resource/n2eg3Zz9/C6gsxh2td3BGrLo7/material-n2eg3Zz9.png, e soprattutto perché i moti per Tolomeo sono descrizioni matematiche che sostanzialmente non differiscono da quelli terrestri, mentre per Aristotele il moto circolare degli astri è una descrizione fisica e qualitativamente diversa dai moti che caratterizzano la fisica terrestre che sarebbero esclusivamente rettilinei uniformi in virtù della teoria dei luoghi naturali. https://i.ytimg.com/vi/2e15A_C_peA/mqdefault.jpg
Secondo Tolomeo le ipotesi astronomiche non sono nozioni che riguardano la natura delle cose. Non è necessario che esse siano dedotte da dei principi della fisica, né che esse si accordino con questi principi metafisici; non è necessario neppure che siano rappresentati come un assemblaggio di corpi solidi che ruotano l’uno in rotazione con l’altro, essi sono pure finzioni geometriche e non hanno altro oggetto che salvare le apparenze dei fenomeni (Vescovini Federici G., I sistemi del mondo) https://www.ibs.it/images/9788889526255_0_424_0_75.jpg
L’astronomia di cui parla Tolomeo dunque non ci fornisce l’essenza delle cose, ma si accontenta di dare un’immagine verosimile e approssimata dei fenomeni. Così mentre il sistema di Aristotele era una descrizione fisico-metafisica della realtà, il sistema astronomico di Tolomeo era una descrizione matematica volta a rispondere alla domanda di Platone ai suoi allievi:
Quali sono i movimenti circolari, uniformi e perfettamente regolari che conviene prendere come ipotesi per poter salvare le apparenze presentate dai pianeti? (Simplicio, Commento al De Caelo di Aristotele).
L’opera più famosa di Tolomeo, ne scrisse molte altre, è l’Almagesto, chiamato così probabilmente dalla parola magìste (più grande) che poi gli arabi, grazie ai quali l’opera si è conservata, tradussero con al-Magisti da cui appunto Almagesto. In realtà il suo nome originario era Mathematiké syntaxis. L’opera rimase sconosciuta per gran parte del medioevo e fu reintrodotta in latino in Europa grazie a Gerardo da Cremona. L’opera conta 30 libri e si presenta come un tentativo di perfezionare ed ampliare l’opera di Ipparco. All’opera è accluso un catalogo stellare che conta oltre alle stelle già catalogate da Ipparco circa ulteriori 150 stelle.
La prima parte della sua opera è dedicata alla ricapitolazione degli assunti fondamentali dell’astronomia secondo cui: il cielo è una sfera che ruota intorno a un asse fisso, così come è chiaro dal movimento delle stelle circumpolari e dal sorgere e tramontare delle astri sempre nei medesimi punti; la Terra è una sfera collocata al centro del mondo ed è come un punto rispetto alle dimensioni del cielo, così che le stelle ci appaiono sempre della stessa grandezza al variare del punto di osservazione del globo; la Terra non ha alcun moto di traslazione. Tolomeo, per spiegare i moti planetari, riprende la teoria di Ipparco e di Apollonio. https://edu.inaf.it/wp-content/uploads/2021/03/sistema_tolemaico01.png Egli utilizza l’eccentrico con il quale un moto apparente non uniforme di un pianeta è ridotto a un moto uniforme intorno ad un centro diverso da quello della Terra. Per i moti più complessi Tolomeo ricorre a un epiciclo posto su un deferente (cioè una circonferenza che si muove attorno alla Terra), così che il differente moto del pianeta è dato dal fatto che quando questo si trova all’esterno dell’epiciclo la sua velocità si aggiunge a quella del deferente (ostentando un’accelerazione); al contempo, quando è all’interno dell’epiciclo, la velocità si sottrae al quella opposta del deferente (e in certi casi può sembrare un moto retrogrado). In aggiunta a questi, al fine di spiegare moti ancora più irregolari, Tolomeo aggiunge l’equante che risulta essere una variazione dell’eccentrico, il “punto equante” è in sostanza un punto diverso sia dal centro dell’orbita sia dal luogo dove risiede la terra, rispetto ad esso il centro dell’epiciclo si muove di moto angolare uniforme.
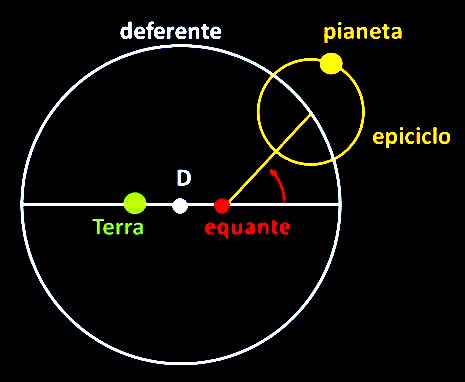L’equante ha come funzione quella di rendere «uniforme il moto angolato», cioè un pianeta copre angoli uguali in tempi uguali, ma non rispetto al centro della circonferenza ma rispetto ad un punto posto sulla retta che congiunge il centro del cerchio alla Terra. Quest’ultimo, combinato con gli eccentrici e gli epicicli, dava ragione delle irregolarità di Marte, Giove e Saturno. Vale anche la pena notare che a differenza del sistema aristotelico, il Sole pur essendo in moto intorno alla terra occupa una posizione centrale nel cosmo e questa posizione fu di stimolo al pensiero copernicano.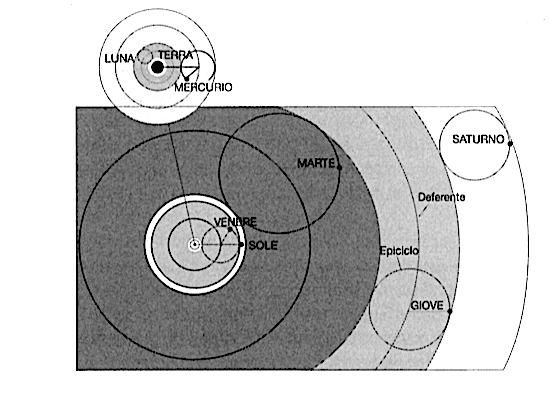
Il sistema tolemaico nel suo complesso risultava insostenibile dal punto di vista fisico, ma ineccepibile dal punto di vista matematico (che come detto era ciò che importava a tutti gli astronomi dell’epoca). Esso rappresentava in quasi tutti i particolari (a parte le variazioni dell’orbita lunare) i moti planetari, tanto che può essere considerato, alla luce dei semplici strumenti in dotazione all’epoca per osservare i moti planetari, un «monumento duraturo per le grandi menti matematiche dalle quali fu gradualmente sviluppato». https://logarithmichistory.files.wordpress.com/2015/11/ptolemy.jpg?w=625
Conseguente all’Almagesto Tolomeo scrive il Tetrabiblos o Quadripartito, così chiamato perché diviso in quattro parti, in quest’opera Tolomeo evidenzia la legittimità e i limiti delle previsioni astrologiche che sono considerati probabili pronosticon sulla base del moto dell’astro da cui dipendono. https://cultura.biografieonline.it/wp-content/uploads/2012/10/zodiac_constellations.jpg L’astrologia dunque per Tolomeo seve a fare previsioni astronomiche grazie alla sintassi matematica, il Mathematiké syntaxis, pertanto l’astronomia matematica e l’astrologia matematica hanno la stessa base, sono due facce della stessa medaglia, e va subito precisato che l’astrologia matematica di cui parla Tolomeo che si avvale della matematica dell’Almagesto cioè degli eccentrici e degli epicicli non ha nulla a che fare con le pratiche divinatorie o con la formulazione di giudizi infallibili; senza entrare nei particolari il rapporto tra astrologia e astronomia spesso è stato frainteso proprio perché non ha tenuto conto della base matematica che Tolomeo gli aveva attribuito, come ben evidenziato negli studi della storica della
scienza e della filosofia Graziella Vescovini Federici.
Video sintesi delle tre lezioni sull'astronomia matematica: Apollonio, Ipparco e Tolomeo
Il moto retrogrado dei pianeti spiegato con l'epiciclo di Ipparco e Tolomeo